目の前にある紙を黄金比に切ることになったとする。定規もコンパスもない。ハサミか手で切らないといけない。さてどうするか。
黄金比?
黄金比とは何かについてはWikipedia「黄金比」に色々書いてあるので省略。とりあえず \(1\colon\frac{-1+\sqrt{5}}{2}\) であるということを把握しておこう。\(\frac{-1+\sqrt{5}}{2}\)で割れば\( \frac{1+\sqrt{5}}{2}\colon1\)になる。
こんな具合に無限に正方形が切り出せる。ぐるぐるぐる。
細長い紙を短くする場合と正方形に近い紙の端っこを切り落とす場合ので2パターンある。どちらの場合も、重要なポイントは「とりあえず\(\frac{\sqrt{5}}{2}\)を作る」というところ。
あまり細長くない紙の場合
あまり細長くない紙、たとえばA版B版の紙とか、正方形の折り紙とか。
長辺の長さを1とする。短辺が\(\frac{-1+\sqrt{5}}{2}\)になるように上を切り落としたい。
まず長辺を半分に折る。
斜めに折り返して、短辺の1/2のところに印をつける。
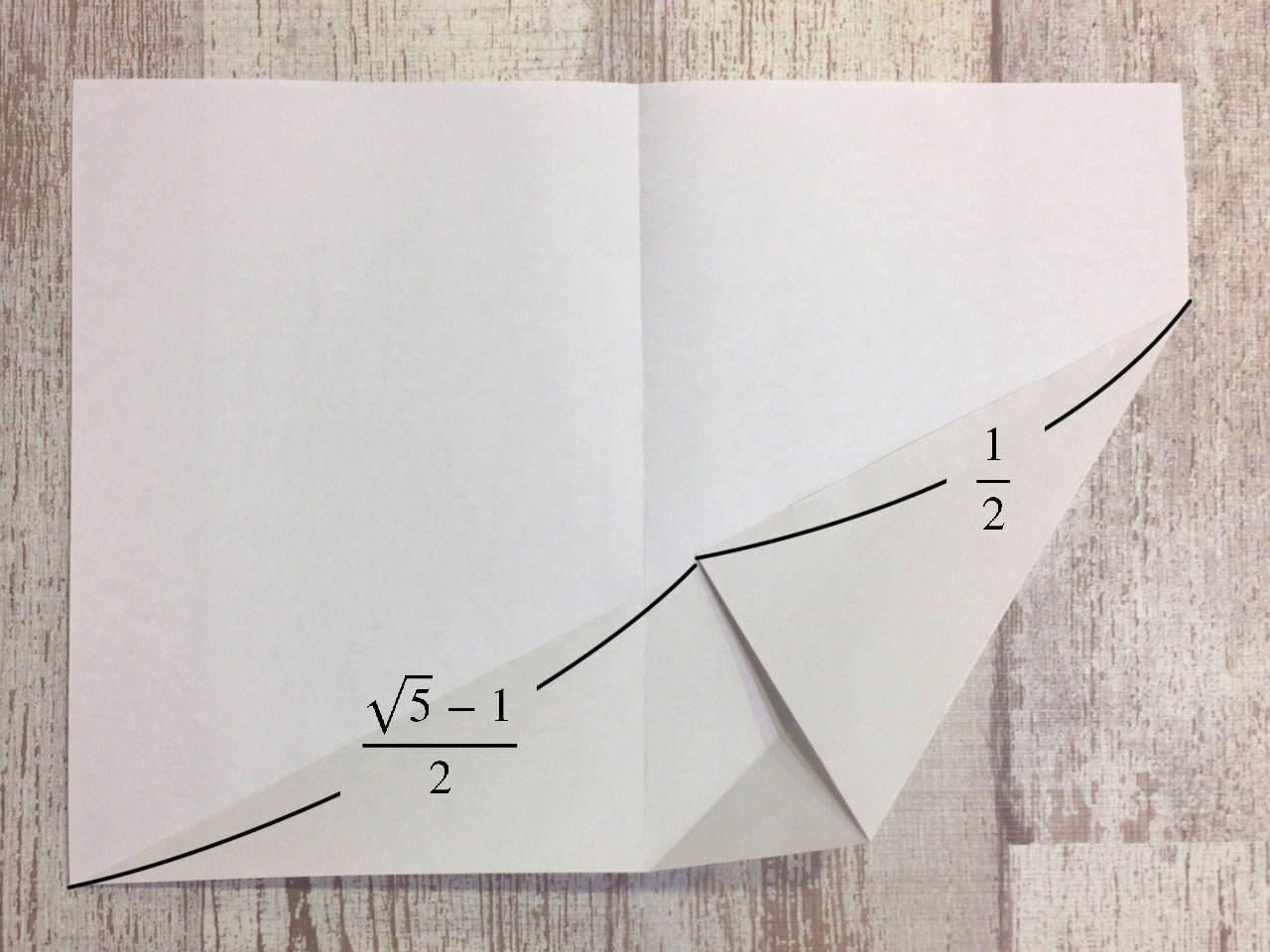
こんなふうに折り返すと\(\frac{\sqrt{5}}{2}\)ができる。
ここから1/2を引けば\(\frac{\sqrt{5}-1}{2}\)が出現する。これだ! これが欲しかったやつだ!
あとは、この長さを短辺にコピーすればいい。
印をつけたら
端っこに折り目をつけて切り落として……
できあがり。
細長い紙の場合
巻紙とかトイレットペーパーといった細長い紙の場合はちょっと別のやり方になる。今度はさっきとは逆に短辺のほうを1として、右端の長過ぎる部分を切り落として\(\frac{1+\sqrt{5}}{2}\)にすることを想定している。
ぺたっと折り返して……
屏風状に折って、1/2幅を3箇所作る。
紙の右側の短辺を縦半分に折って1/2のところにマークをつける。下の図の青い線のところが\(\frac{\sqrt{5}}{2}\)になる。
これを長辺側にコピーしよう。さっきの青い線に向けて長辺を折り返して
折り目をつける。
これで目標の\(\frac{1+\sqrt{5}}{2}\)ができた!
折り目をつけて……
切り落としてできあがり。
なんとなく役に立ちそうな技だが、今まで役に立ったことがない。それでも、自分はいつでもそのへんの紙から黄金比を切り出せるんだという自信を持っていたほうが強く生きられるんじゃないだろうかと思う。